This article is part technical documentation, part feature list and also part FAQ. It intends to explain why Diorama was written the way it was, why `it takes so long' and what it can do that would be extremely hard for other random map generators to achieve.

Diorama aims to create maps that are both strategically appealing and visually appealing. Both aspects are important to a good map, and Diorama treats both properties roughly equal. The approach used to create a map can be described as a top-down approach. First an abstract representation of a map is generated, and then it is fleshed out and refined in stages.

Compare this to a bottom-up approach where the you start with random detail (such as a height map) and then infer overall structure. This approach is much faster, but a significant downside is that it is very hard to guarantee in a natural way certain properties (such as reachability) of the final result - or even to request certain properties.

The main problem with a top-down approach is not coming up with a good abstract map representation (a simple 2d maze will work), but to create said maze in the first place so that it is interesting strategically.

Something that is significant in a map is your starting location. It would be easy to randomly assign a position on the map (and for oil wells as well) and hope it works out. But that won't make for an interesting game necessarily. For instance you might be unlucky and be stuck on a tiny random mountain with no way to do anything. Or very lucky and have all the oil on the map be next to your starting position.

Generally it would be desirable if the player bases are as far apart from each other as possible. For two player bases the solution to this problem is trivial: Opposite corners - if they are both free and not taken up by randomly generated impassable terrain. For four players it might seem obvious that its the four corners -- but what about non-square maps? Eight player maps are even more complicated, and a good solution is non-obvious.

Let's complicate the matters further: Free oil wells are oil wells which do not belong to a player's starting oil wells, i.e. oil wells that are up for grabs. These free oil wells should also be as far apart from each other and each player base as possible. (But this constraint is not quite as important as player bases being as far from each other as possible.)

If we assume we can place things anywhere on the map, then we can lay out the players bases and oil wells in a regular grid and then draw bits around. But this would give boring maps, as they are always more or less the same. On the other hand if we try and put a regular grid over the existing random terrain, we may not be able to get the location we want. Simply not placing the feature is unacceptable, nor is placing it somewhere random.

We could however try every possible combination, measure the minimum distance between each feature, and then pick the one that has the largest minimum distance. However this quickly becomes impractical. On a 12 x 12 map (very small) with 8 player bases and 4 random oil wells we are looking at 103619293824707388 possible combinations to choose 12 locations from a possible 144. Given we can check 10000 of those each second we'd still be looking at roughly 328574 exciting years of computation.

Genetic algorithms do help, but they tend to favour a local minimum and its impossible to know if the solution found is actually the best there is. At this point you could reasonably argue that "who **** cares, its just a warzone map!", but that would lame and we can do better.

This is one of the problems we are attacking with answer set programming (ASP). ASP is a declarative approach to solving search problems, so you write a description of the problem (in a logic like language) and then give this description to a solver (kind of like a theorem prover) which will come up with valid model (solution) of the problem. But not just any solution, we will arrive at the optimal solution, and we can prove that the solution is optimal. The down side is that generating this can take exponential time (this is why requesting very large maps can take a while) but it allows both local ("a base must have a given number of entrances") and global ("every base must be able to reach every other base") conditions on the map to be expressed simply, cleanly and efficiently. Critically we don't have to change any of the algorithms when the conditions on the map change, we just change the description that gets input into the solver.

Another problem is coming up with good random terrain where every significant point of interest is reachable (by walking or driving). Assigning each point a random height and then blurring will give a reasonable result, but it will be uniform in its randomness and won't make for a strategically interesting game.

Terrain should not be flat, but not just random either. There should be clear features, such as (to name a few) winded ramps up to player's bases, hills, canyons, causeways, lakes, and so on. Since warzone only offers us 256 hight levels we can't just draw what we want either. Also, if we start making mountains in one area of the map, we may end up with an stupidly high cliff with no way to connect the two areas of the map.

The entire map is generated from an abstract representation; the main hard part is coming up with a good one. The format is as follows:

3313213i
3@121232
33333123
32011322
32133223
33132333
200223@3
i3221232

Each number represents a cell. (The parameters map cell width and map cell height in diorama influence how large this initial map representation is. The parameter cell scale influences to how many tiles squared (roughly) each cell expands to on the final map.) The numbers represent a cells height with 0 being the lowest and 3 being the highest in this case. The @ symbols indicate a player's starting base, although each player's base also has a height value like any other cell (but it is not shown here). The blue i's indicate the locations where free oil wells should be placed (like player bases, they also have a height value which is not shown in the above diagram).

Cliffs are drawn along edges where there is a difference in height numbers of at least 2. So for example in the first row, there is a cliff between the second and third cell.

This is actually enough to draw a map, but it would end up very blocky:

Figure 1: Map with only straight cliffs.

If we simply jitter each point on the grid a draw cliffs between them we will get a much more natural layout.

Figure 2: Map with jittered cliffs.

This is one example of how the abstract map gets more and more refined.

Another high level feature of a map is roads. There is two approaches to this, roads on urban maps (grid pattern) and roads on arizona and rockies maps (random). Urban roads are much simpler: We simply arrange the roads in a grid, double up some of them (for dual carriage ways) and poke holes into the grid (for the nuclear wasteland look and feel).

Roads on arizona and rockies maps are a bit more interesting. We first decide where to draw roads: Each player base should be connected to a road somehow (as that way you immediately notice the roads and you think 'hey, this is kinda nifty'). We then decided that each oil well cluster should also be connected to a road as they also represent interesting points on the map. Finally, we pick a few (maybe 3) of totally random points on the map and also make sure they are connected to the road network somehow.

We then construct a minimum spanning tree between each of those points and draw a road between them. However, if we apply a standard path-finding algorithm which assumes the cost to go from any one square to an adjacent square is equal, we get a pretty ugly result as shown below:

Figure 3: Standard equal cost path-finding. Roads are highlighted in blue for illustration purposes.

You will notice immediately that roads criss-cross each other, are fairly "square" and generally... quite messy. Not how a civilisation would construct them. If we already have a road somewhere, its better to re-use it as much as possible. Adjusting the path-finding algorithm so that going to any road tile already on the map is significantly cheaper will give a result as shown below:

Figure 4: Re-used roads.

However, just finding the shortest distance does not give a realistic result, so will be slightly more random in how we compute the `shortest' path. Thus in our path-finding algorithm we have a very low cost associated with going to a tile that already contains a road, and we have a high (and a little bit random) cost associated for choosing a non-road tile. The result is a fairly natural looking network of paths, twisting and turning but ultimately reaching each target in a fairly efficient manner, as shown below:

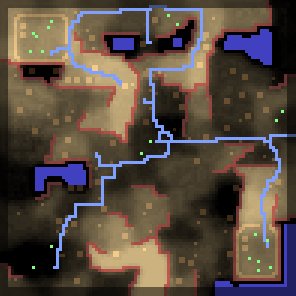
Figure 5: Jittered roads.

By default the map will just be covered in the same texture (red sand for example). We then further refine the map by splatting random textures across it.

There are technical difficulties, such as correctly drawing all the transitions between one terrain style and another (and not all transitions are possible), but these are implementation details.

This is another area we use ASP. We have a model of a good player base, which is basically: Buildings should be aligned in a grid, there must be a gap between them, the base overall should leave as many rows and columns free (i.e. lots of straights with empty tiles without buildings on them).

Around the base a wall is drawn and a hole is poked in it to give you an entrance.

The reason we don't just have a pre-defined model of a base and just place it on the map is that we don't really know what kind of terrain will be around a player base: There may be cliffs in inconvenient places. The ASP will work around those and will give us a good model regardless.

Finally, we place neutral features on the map: Buildings on the urban maps, rocks and scavenger villages for arizona maps, and trees and huts on rockies maps.

We're slightly more clever in how to place them by making use of all the information we have generated in earlier stages: For example on urban maps, buildings are placed next to roads; on arizona maps we place the scavenger towns in a circle around any of the roads; on rockies maps we place trees on non-snow terrain and snowy trees on snowy terrain.